RECORD AI
6. Dropout Regularization (드롭아웃 정규화) 본문
Dropout Regularization
1. Dropout
L2 Regularization 외에 또 다른 매우 강력한 정규화 기법으로
드롭아웃(Dropout Regularization)이 있다. 어떻게 작동하는지 알아보자.

위와같은 과적합(overfitting)된 신경망을 훈련시킨다고 할때
드롭아웃의 방식이란,
신경망 각각의 층에 대해 노드를 삭제하는 확률을 설정하는것이다.
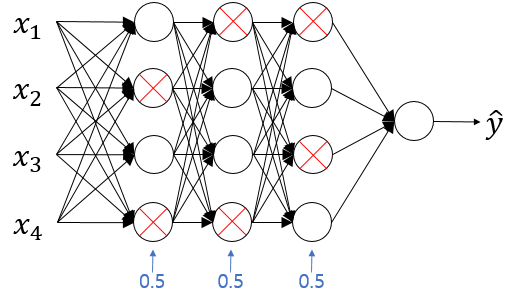
이와같이 0.5로 설정하고 각각의 층에 대해 각 노드마다 동전을 던지면
0.5의 확률로 해당 노드를 유지하고, 0.5의 확률로 노드를 삭제하게 된다.

동전을 던져 각각의 노드를 삭제하고 삭제된 노드에
들어가는 링크와 나가는 링크를 모두 삭제하면
위와같은 더 작고 간소화된 네트워크가 된다.
그리고 감소된 네트워크에서 하나의 샘플을 back propagation으로 훈련시키고
다른 샘플에 대해서도 동전을 던지고 다른 세트의 노드들을 남기고
다른 세트의 노드들은 삭제하게 된다.
이렇게 각각의 훈련 샘플에 대해서 감소된 네트워크를 사용해 훈련하게된다.
그러면 왜 신경망을 정규화 할 수 있는지에 대해서 직관적으로 알 수 있게된다.
즉, 더 작은 네트워크를 훈련시키기 때문이다.
드롭아웃을 실제로 어떻게 구현하는지
역 드롭아웃(Inverted dropout)이라는 기법을 통해 살펴보자.
2. Implementing dropout("Inverted dropout")
layer $l = 3$
직관적인 이해를 위해 층이 3개인 경우를 예시로 살펴보자.
먼저 층3에 대한 드롭아웃 벡터인 무작위 랜덤 벡터 $d3$를 설정한다.
keep_prob = 0.8
d3 = np.random.rand(a3.shape[0],a3.shape[1]) < keep_prob
$d3$은 $a3$와 같은 모양을 가지게 된다.
그리고 keep_prob이라는 숫자보다 작은지 비교한다.
위에서는 0.5로 지정했지만 keep_prob을 여기서는 0.8로 설정한다.
이 수는 주어진 은닉 유닛이 유지될 확률이다.
keep_prob이 0.8 이라는 것은 어떤 은닉 유닛이 삭제될 확률이 0.2 라는 뜻이다.
따라서 이 $d3$는 keep_prob과 비교하여
0.8의 확률로 1의 값을 가지고 (true),
0.2의 확률로 0의 값을 가지는 (false) 행렬이 된다.
다음으로 3번째 층의 활성화값인 $a3$에 대한 코드를 작성하면
a3 = np.multiply(a3,d3) # a3*d3위와같이 $a3$는 예전 $a3$의 값에 $d3$를 요소별곱셈(elementwise)을 해준것이다.
$a3*d3$ 로 써도 된다.
모든 원소에 대해 20퍼센트의 확률로 0이 되는 $d3$의 원소를 곱해
대응되는 $a3$의 원소들을 0으로 만들게 된다.
파이썬에서 $d3$는 True와 False의 값을 갖는 불(bool)타입의 행렬이 될것이다.
a3 /= keep_prob그리고 최종적으로 얻는 $a3$를 0.8로 나누어준다.
keep_prob 파라미터로 나눠주는것이다.
이 마지막단계를 설명하자면 예를들어 세번째 은닉층에 50개의 유닛,
50개의 뉴런이 있다고 해보자.
그럼 $a3$는 $(50,1)$ 차원일 것이고 Vectorization되었다면 $(50,m)$일 것이다.
80%의 확률로 유지하고 20%의 확률로 삭제한다면
평균적으로 10개의 유닛이 삭제된다. (즉 0의 값을 갖게 된다.)
$z^{[4]}$의 값을 살펴보면 $z^{[4]} = w^{[4]}a^{[3]} + b^{[4]}$와 같다.
예상대로 이 값은 20% 줄어들게 된다.
$a3$ 원소의 20%가 0이 된다는 의미이다.
따라서 $z^{[4]}$의 기댓값을 줄이지 않기위해 0.8로 나눠줘야한다.
($\div 0.8$ 한다는것은 $= \times \frac{5}{4} = \times 1.25$와 같다.)
왜냐하면 필요한 20%정도의 값을 다시 원래대로 만들어줄 수 있기 때문이다.
이를 통해 $a3$의 기댓값을 유지할 수 있다.
a3 /= keep_prob
따라서 이것이 역 드롭아웃(Inverted dropout)이라고 불리는 기법이다.
keep_prob값을 0.8 , 0.9 어떤 값으로 설정하든 다시 나눠줌으로써
$a3$의 기댓값을 같게 유지시켜주는것이다.
그리고 신경망을 평가하는 과정에서 이 역 드롭아웃기법이
테스트를 더욱 쉽게 만들어준다. 스케일링 문제가 적기 때문이다.
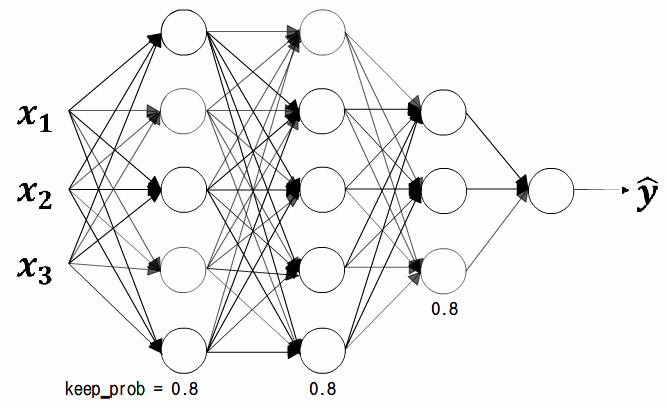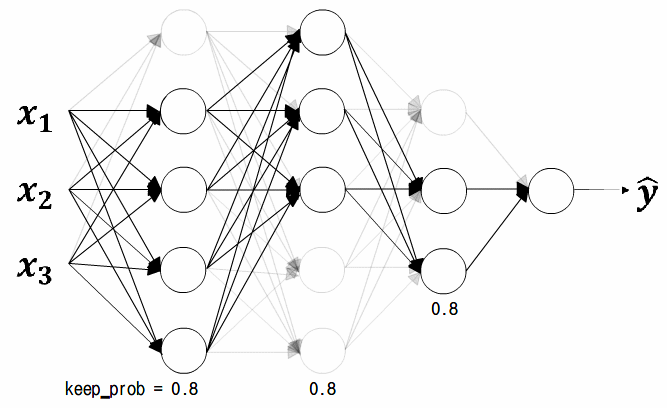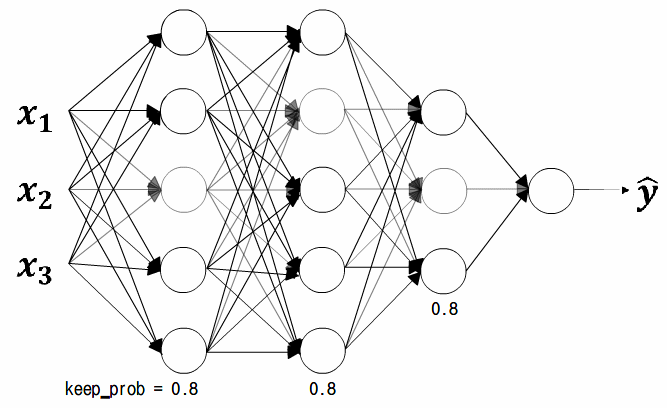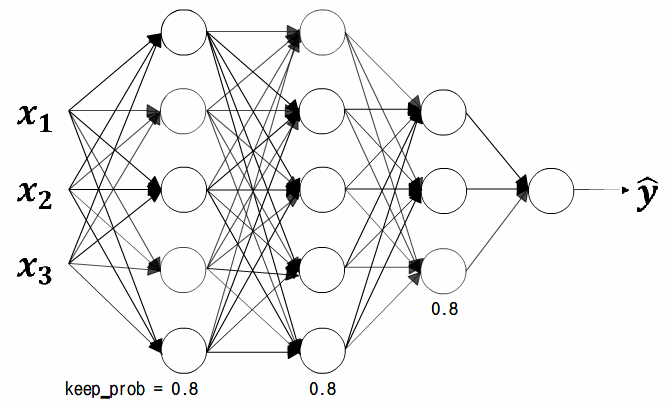
역 드롭아웃은 가장 보편적인 드롭아웃 기법이다.
keep_prob으로 나누는 것을 빼고 훈련 반복을 하면
테스트할때 알고리즘이 더 복잡해진다.
위에 소개된 방법이 가장 보편적이다.
$d$벡터를 사용해 서로 다른 훈련 샘플마다 다른 은닉 유닛들을 0으로 만든다.
같은 훈련 세트를 통해 여러번 반복하면 반복마다 0이 되는 은닉 유닛은 무작위로 달라지게 된다.
따라서 하나의 샘플에서 계속 같은 은닉 유닛을 0으로 만드는것이 아닌
경사하강법의 반복마다 0이 되는 은닉 유닛들이 달라진다.
즉, 같은 훈련세트를 두번째로 반복할때
0이 되는 은닉 유닛의 패턴은 달라지게 된다.
세번째 층의 $d3$벡터는 foward propagation과 backward propagation 모두에서
어떤 노드를 0으로 만들지 결정하게된다.
3. Making predictions at test time
테스트에서는 드롭아웃을 사용하지 않는다.
$X = a^{[0]}$
$X$라는 샘플이 주어질때, 이것을 0번째 층의 활성화값 $a^{[0]}$으로 표현해준다.
그리고
$z^{[1]} = w^{[1]} a^{[0]} + b^{[1]} $
$a^{[1]} = g^{[1]}(z^{[1]})$
$z^{[2]} = w^{[2]} a^{[1]} + b^{[2]} $
$a^{[2]} = … $
와 같은 방식으로 마지막 층에 이르러 예측값 $\hat{y}$을 얻는다.
테스트에서는 결과가 무작위로 나오는것을 원하지않기때문에 드롭아웃을 사용하지않는다.
테스트에 드롭아웃을 구현하는것은 노이즈만 증가시킬 뿐이다.
드롭아웃을 구현하지않았기때문에 활성화 기대값의 크기가 변하지않는다.
따라서 테스트에서 keep_prob으로 나눠주지 않아도 된다.
이렇게 드롭아웃이라는 기법을 알아보았다.
참조 1
'Deep Learning > improving DNN' 카테고리의 다른 글
| 8. Other_Regularization_Methods (1) | 2022.12.26 |
|---|---|
| 7. Understanding Dropout (0) | 2022.12.26 |
| 5. Why Regularization Reduces Overfitting (0) | 2022.12.26 |
| 4. Regularization (정규화) (0) | 2022.12.26 |
| 3. Basic Recipe for Machine Learning (0) | 2022.12.26 |


